Auf dieser Seite:
Möchtest Du die 100 Aufgaben des kleinen auswendig lernen, dann ist das eine Menge (unnötige) Arbeit!
Ein paar Rechentricks machen das Leben deutlich einfacher! 😉
Einmaleins-Rechentrick: Tauschaufgabe
Wie auch schon bei den Plus-Rechnen Tauschaufgaben, kann man auch bei den Mal-Aufgaben die beiden Faktoren vertauschen, ohne dass sich das Ergebnis ändert.
Zum Beispiel:
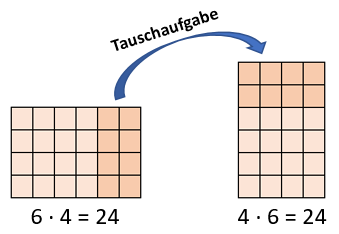
6 ⋅ 4 ergibt ebenso wie 6 ⋅ 4 das Ergebnis 24. Auf dem Bild siehst Du, dass die Kästchen einfach nur gedreht beziehungsweise „aufgestellt“ wurden. Die Anzahl ändert sich dadurch natürlich nicht.
Das gleiche gilt selbstverständlich auch für alle anderen Mal-Aufgaben.
Tauschaufgaben der Multiplikation
Bei der Multiplikation (=mal rechnen) ist die Reihenfolge, der malzunehmenden Zahlen (= Faktoren) egal!
Hinweis: Diese Regel lernst Du später auch als Kommutativgesetz der Multiplikation kennen.
Achtung: Für die Subtraktion (minus rechnen) und Division (teilen) geht das nicht – nur für Addition (plus rechnen) und Multiplikation (mal nehmen)!
Tauschaufgaben und Umkehraufgaben
Achtung: Die Begriffe Tauschaufgabe und Umkehraufgabe lernen zwar schon die Schüler der Klasse 1 kennen, werden aber oft verwechselt.
Tauschaufgaben sind immer von der gleichen Art (plus oder mal), nur die Operanden werden getauscht, das Ergebnis ist gleich: 2 ⋅ 6 = 12 und 6 ⋅ 2 = 12
Umkehraufgaben werden für die „Gegenrechnung“ oder „Probe“ verwendet. Sie sind von der entgegengesetzten Art (plus -> minus, mal -> geteilt) und beginnen mit dem Ergebnis. Das Ergebnis der Umkehraufgabe ist der andere Operand: 2 ⋅ 6 = 12 -> 12 : 6 = 2
Einmaleins-Rechentrick: Nachbaraufgaben
Bei den Erklärungen zu den einzelnen Reihen des kleinen Einmaleins wird dargestellt, wie sich die Malaufgaben in Plusaufgaben umwandeln lassen.
Ein Beispiel aus der 7er-Reihe:
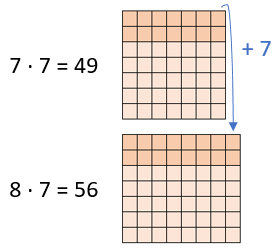
| 7 ⋅ 7 | = 7 + 7 + 7 + 7 + 7 + 7 + 7 | = 49 |
| 8 ⋅ 7 | = 7 + 7 + 7 + 7 + 7 + 7 + 7 + 7 | = 56 |
Mit jeder Aufgabe kommen im Vergleich zur vorhergehenden Aufgabe 7 Kästchen dazu, also „immer +7„.
Das nutzen wir aus:
Ist die Aufgabe zum Beispiel 8 ⋅ 7 und Du weißt, dass 7 ⋅ 7 = 49. Das Ergebnis ist dann genau um 7 größer, also 49 + 7 = 56.
Das Ganze funktioniert natürlich auch in die andere Richtung – ist die Aufgabe zum Beispiel 6 ⋅ 7 und Du weißt, dass 7 ⋅ 7 = 49. Das Ergebnis ist dann genau um 7 kleiner, also 49 – 7 = 42.
Einmaleins-Rechentrick: Verdoppeln / Halbieren
Wird bei Mal-Aufgaben einer der beiden Faktoren verdoppelt, dann verdoppelt sich auch das Ergebnis.
Umgekehrt: Wird bei Mal-Aufgaben einer der beiden Faktoren halbiert, dann halbiert sich auch das Ergebnis.
Zum Beispiel:
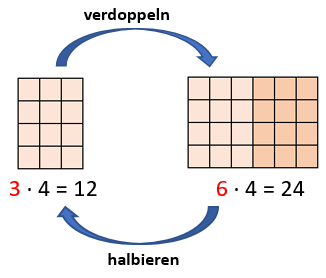
Verdoppelt man in der Aufgabe 3 ⋅ 4 den ersten Faktor 3, dann erhält man die Aufgabe 6 ⋅ 4. Das Ergebnis verdoppelt sich dann von 12 auf 24.
Man kann Verdoppeln und Halbieren auch kombinieren, so dass sich beides aufhebt und sich das Ergebnis nicht ändert: Weiß man das Ergebnis 6 ⋅ 4 = 24, dann ist auch 3 ⋅ 8 = 24, denn 3 ist die Hälfte von 6 und 8 ist das Doppelte von 4.
Einmaleins-Rechentrick: Quadratzahlen
Bei den Quadratzahlen handelt es sich streng genommen nicht um einen Rechentrick, aber Du solltest sie gut auswendig lernen, da Du sie insbesondere mit dem Trick Nachbaraufgaben kombinieren kannst.
Die Quadratzahlen sind auch Voraussetzung für den folgenden Rechentrick „fast Quadratzahl“.
Alles zu den Quadratzahlen selbst, inklusive einem coolen Rap um sie zu lernen, findest Du auf der Seite Einmaleins Quadratzahlen.
Einmaleins-Rechentrick: „fast Quadratzahl“
Kannst Du gut die Quadratzahlen, dann kannst Du diesen Rechentrick anwenden um zum Beispiel die Aufgaben 6 ⋅ 8 oder 7 ⋅ 9 ganz einfach zu lösen!
Bei „fast Quadratzahlen“ ist ein Faktor um 1 größ und der andere Faktor um 1 kleiner als bei einer Quadratzahl-Aufgabe → der Abstand ist genau 2.
Das Ergebnis ist dann genau um 1 kleiner als das Ergebnis der zugehörigen Quadratzahlaufgabe!
Beispiel 1:
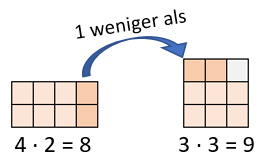
Nimmt man bei der Aufgabe 4 ⋅ 2 das letzte „2er-Päckchen“ ganz rechts und verschiebt es nach oben (dunkel-orange), dann fehlt genau noch 1 Kästchen zur Aufgabe 3 ⋅ 3.
Weißt Du nun in die Quadrat-Aufgabe 3 ⋅ 3 = 9, dann ist das Ergebnis von 4 ⋅ 2 genau um 1 kleiner, also 9 – 1 = 8.
Beispiel 2:
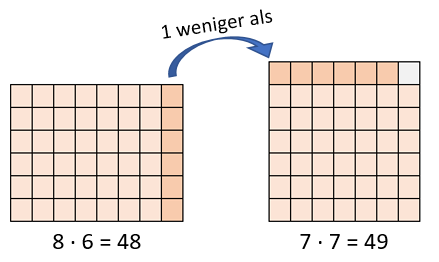
Nimmt man bei der Aufgabe 8 ⋅ 6 das letzte „6er-Päckchen“ ganz rechts und verschiebt es nach oben (dunkel-orange), dann fehlt genau noch 1 Kästchen zur Aufgabe 7 ⋅ 7.
Weißt Du nun in die Quadrat-Aufgabe 7 ⋅ 7 = 49, dann ist das Ergebnis von 6 ⋅ 8 genau um 1 kleiner, also 49 – 1 = 48.
Kleines Einmaleins (1 x 1) – Online Trainer
Mit dem Einmaleins (1 x 1) – Online Trainer kannst Du das kleine Einmaleins schnell und selbstständig üben.
Wähle, welche Aufgaben Du üben möchtest und schon geht’s los!
Je nachdem, wie schnell Du die Lösung weißt und ob Du sie richtig hast, wird immer die passende Aufgabe ausgewählt.
