Schriftlich Addieren – Erklärung

Schriftliche Addition – wofür?

Möchte man große Zahlen addieren (= plus rechnen), dann ist es schwierig diese Berechnung im Kopf durchzuführen. Ebenso ist es oft schwierig, wenn man mehr als zwei Zahlen addieren möchte.
Hat man gerade „Papier und Bleistift“ zur Hand, dann lassen sich diese Probleme lösen, wenn man die schriftliche Addition beherrscht.

Schriftliche Addition – Idee

Zahlen lassen sich an Hand ihrer Ziffern in Einer, Zehner, Hunderter, usw. „zerlegen“. Zum Beispiel:
648 = 6 Hunderter + 4 Zehner + 8 Einer
435 = 4 Hunderter + 3 Zehner + 5 Einer

Bei der schriftlichen Addition beginnt man, indem man von allen Summanden (= Zahlen, die man zusammenrechnet) zunächst jeweils nur die Einerstelle zusammenrechnet. Das Ergebnis dieser Nebenrechnung entspricht dann der Einerstelle des Ergebnisses. Nach dem gleichen Prinzip berechnet man die Zehner, Hunderter, usw. des Ergebnisses. Ganz einfach eigentlich, oder? Fast…

Schriftliche Addition – Übertrag

Rechnet man die Ziffern einer einzelnen Stelle zusammen, kommt es vor, dass das Ergebnis größer als 9 ist, also eine zweistellige Zahl.

8 + 5 = 13 Einer lassen sich aber schlecht ins Ergebnis schreiben… Also nimmt man hiervon sofort 10 Einer weg und bündelt diese zu einem Zehner! Die verbleibenden 3 Einer schreibt man ins Ergebnis. Der gebündelte Zehner fließt als Übertrag in die Berechnung der Zehnerstelle ein.

Nach dem gleichen Prinzip bündelt man in den folgenden Schritten jeweils 10 Zehner zu einem Hunderter, 10 Hunderter zu einem Tausender, usw.

Aus diesem Grund ist es wichtig, bei der schriftlichen Addition mit der Einerstelle zu beginnen!

Schriftliche Addition – Beispiel

Die schriftliche Addition ist somit komplett beschrieben. Wichtig ist noch, dass man die Berechnung in einer bestimmten Form notiert. Am besten lässt sich alles noch einmal an Hand eines Beispiels zeigen:

Start: Schreibe die Aufgabe auf

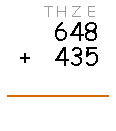
Schreibe die Summanden so untereinander, dass jeweils alle Einerstellen, Zehnerstellen, usw. untereinander stehen. Schreibe ein „+“ vor alle Zahlen, die zur ersten addiert werden sollen.

Schließe das Ganze mit einem Strich ab, unter dem Du dann die Summe berechnen kannst (darüber etwas Platz für überträge lassen).

Für dieses Beispiel sind die Spalten mit E (für Einer), Z (für Zehner), H (für Hunderter) und T (für Tausender) überschrieben. Das macht man nicht, hilft aber hier zur Erklärung.

Schritt 1: Berechne die Einer

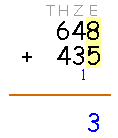
Beginne nun, indem Du von allen Summanden die Einer zusammenrechnest.

Nebenrechnung: 8 + 5 = 13

Das gesuchte Ergebnis hat also 13 Einer. Nimm hiervon 10 Einer und bündele sie zu einem Zehner. Schreibe diesen als Übertrag in die Zehnerspalte. Die verbleibenden 3 Einer schreibe an die entsprechende Stelle ins Ergebnis.

Schritt 2: Berechne die Zehner

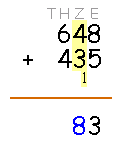
Berechne als nächstes die Zehner, indem Du von allen Summanden die Zehner zusammenrechnest. Denke dabei auch an den Übertrag aus der Berechnung der Einer!

Nebenrechnung: 4 + 3 + 1 = 8

Das Ergebnis hat also 8 Zehner. Schreibe sie an die entsprechende Stelle. Einen Übertrag gibt es diesmal nicht.

Schritt 3: Berechne die Hunderter

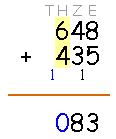
Berechne die Hunderter, indem Du von allen Summanden die Hunderter zusammenrechnest.

Nebenrechnung: 6 + 4 = 10

Das Ergebnis hat 10 Hunderter. Bündele diese zu einem Tausender und schreibe ihn als Übertrag in die Tausenderspalte. Es bleibt kein Hunderter mehr übrig, schreibe also eine 0 in die Hunderterspalte.

Schritt 4: Berechne die Tausender

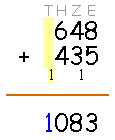
In der Tausenderspalte steht in diesem Fall nur der Übertrag aus dem vorhergehenden Schritt, so dass Du keine große Nebenrechnung brauchst.

Schreibe den Tausender in die entsprechende Spalte ins Ergebnis.

Ende: Lies das Ergebnis ab

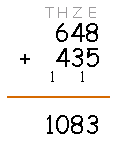
Herzlichen Glückwunsch, Du hast das Ergebnis nun vollständig berechnet!

Das Ergebnis ist 1083.