Schriftlich Multiplizieren (mehrstellig) – Erklärung

Schriftliche Multiplikation – wofür?

Möchte man große Zahlen multiplizieren (= mal rechnen), dann ist es schwierig diese Berechnung im Kopf durchzuführen. Hat man aber gerade "Papier und Bleistift" zur Hand, dann lassen sich diese Probleme lösen, wenn man die schriftliche Multiplikation beherrscht.

Hier geht es um den komplizierteren Fall, dass zwei mehrstellige Faktoren (= Zahlen, die malgenommen werden) miteinander multipliziert werden sollen.

Link: Multiplikation einer mehrstelligen Zahl mit einer einstelligen Zahl

Schriftliche Multiplikation – Idee

Zahlen lassen sich an Hand ihrer Ziffern in Einer, Zehner, Hunderter, usw. "zerlegen".

Zum Beispiel:
391 = 3 Hunderter + 9 Zehner + 1 Einer
235 = 2 Hunderter + 3 Zehner + 5 Einer

Die schriftliche Multiplikation von mehrstelligen Zahlen wird zurückgeführt auf mehrere Multiplikationen mit einer einstelligen Zahl. Die Teilergebnisse werden anschließend schriftlich addiert (= plus rechnen).

Beispiel:
  391 * 235
= 391 * (2 Hunderter + 3 Zehner + 5 Einer)
= 391 * 2 Hunderter + 391 * 3 Zehner + 391 * 5 Einer

Schriftliche Multiplikation – Beispiel

Die schriftliche Multiplikation mit mehrstelligen Zahlen ist somit komplett beschrieben. Wichtig ist noch, dass man die Berechnung in einer bestimmten Form notiert. Am besten lässt sich alles noch einmal an Hand eines Beispiels zeigen:

Start: Schreibe die Aufgabe auf

Schreibe die Aufgabe auf. Statt eines "=" ziehe aber einen Strich unter die Aufgabe. Hier schreibst Du zunächst die Zwischenergebnisse der einzelnen Teilmultiplikationen hin.

Für dieses Beispiel sind die Spalten für das Ergebnis mit E (für Einer), Z (für Zehner), H (für Hunderter) und T (für Tausender) überschrieben. Das macht man nicht, hilft aber hier zur Erklärung.

Schritt 1: Multipliziere mit den Hundertern

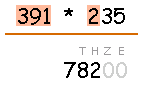
Beginne nun, indem Du den ersten Faktor 391 mit der Hunderterstelle des zweiten Faktors (= 2 Hunderter) multiplizierst. Gehe hierbei vor wie unter Multiplikationen mit einer einstelligen Zahl beschrieben.

Nebenrechnung: 391 * 2 = 782 (animierte Musterlösung)

Das erste Teilergebnis sind 782 Hunderter (= 7 Zehntausender + 8 Tausender + 2 Hunderter). Trage es in den richtigen Spalten ein, wenn Du möchtest kannst Du der Vollständigkeit halber für die Zehner und Einer eine 0 eintragen.

Schritt 2: Multipliziere mit den Zehnern

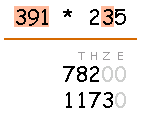
Multipliziere den ersten Faktor 391 mit der Zehnerstelle des zweiten Faktors (= 3 Zehner). Gehe wieder vor wie unter Multiplikationen mit einer einstelligen Zahl beschrieben.

Nebenrechnung: 391 * 3 = 1173 (animierte Musterlösung)

Das zweite Teilergebnis sind 1173 Zehner (= 1 Zehntausender + 1 Tausender + 7 Hunderter + 3 Zehner). Trage es in den richtigen Spalten ein, wenn Du möchtest kannst Du der Vollständigkeit halber für die Einer eine 0 eintragen.

Schritt 3: Multipliziere mit den Einern

Multipliziere den ersten Faktor 391 mit der Einerstelle des zweiten Faktors (= 5 Einer). Gehe auch diesmal vor wie unter Multiplikationen mit einer einstelligen Zahl beschrieben.

Nebenrechnung: 391 * 5 = 1955 (animierte Musterlösung)

Das dritte und letzte Teilergebnis sind also 1955 Einer (= 1 Tausender + 9 Hunderter + 5 Zehner + 5 Einer). Trage auch dies in den entsprechenden Spalten ein.

Schritt 4: Addiere die Teilergebnisse

Zur Erinnerung:
  391 * 235
= 391 * (2 Hunderter + 3 Zehner + 5 Einer)
=   391 * 2 Hunderter (Schritt 1)
  + 391 * 3 Zehner (Schritt 2)
  + 391 * 5 Einer (Schritt 3)

Die in den Schritten 1-3 berechneten Teilergebnisse müssen also noch zusammenaddiert werden. Dadurch, dass die Zahlen bereits Stellengerecht untereinanderstehen, ist das direkt durch eine schriftliche Addition möglich.

Nebenrechnung: 78200 + 1173 + 1955 = 91885 (animierte Musterlösung)

Ende: Lies das Ergebnis ab

Herzlichen Glückwunsch, Du hast das Ergebnis nun vollständig berechnet!

Das Ergebnis ist 91885.