
Beispiel für eine Tauschaufgabe
Mona möchte sich Sticker kaufen, sie kosten 2 Euro. Danach findet sie noch ein schönes „Malen nach Zahlen“ für 6 Euro. Wieviel kostet nun beides zusammen?
6 + 2 = 8 kann Mona schnell ausrechnen, das geht einfach! Aber hier muss man doch 2 + 6 rechnen – oder ist das egal?
Ja, es ist egal:
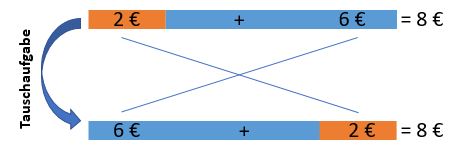
Rechentrick: Tauschaufgabe
Bei der Addition (=plus rechnen) ist die Reihenfolge, der zu addierenden Zahlen egal!
Hinweis: Tauschaufgaben ergeben später auch bei der Multiplikation (mal rechnen) das selbe Ergebnis -> Kommutativgesetz
Achtung: Für die Subtraktion (minus rechnen) und Division (teilen) geht das nicht.
Wofür Tauschaufgaben?
Meistens ist es einfacher, die kleinere Zahl zu der größeren Zahl hinzuzurechnen. Das ist vor allem dann der Fall, wenn der Unterschied der zu addierenden Zahlen groß ist. Besonders, wenn eine der zu addierenden Zahlen sehr klein ist.
Ist das der Fall, kann man stattdessen das Ergebnis der Tauschaufgabe berechnen.
Tauschaufgaben und Umkehraufgaben
Achtung: Die Begriffe Tauschaufgabe und Umkehraufgabe lernen zwar schon die Schüler der Klasse 1 kennen, werden aber oft verwechselt.
Tauschaufgaben sind immer von der gleichen Art (plus oder mal), nur die Operanden werden getauscht, das Ergebnis ist gleich: 2 + 6 = 8 und 6 + 2 = 8
Umkehraufgaben werden für die „Gegenrechnung“ oder „Probe“ verwendet. Sie sind von der entgegengesetzten Art (plus -> minus, mal -> geteilt) und beginnen mit dem Ergebnis. Das Ergebnis der Umkehraufgabe ist der andere Operand: 2 + 6 = 8 -> 8 – 2 = 6
